Abstract
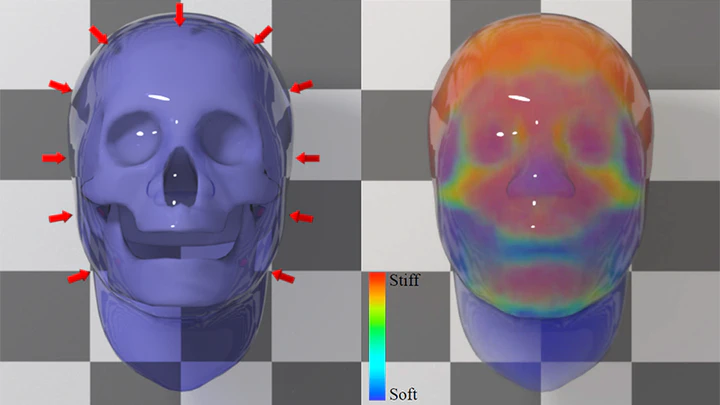
Elastic parameter optimization has revealed its importance in 3D modeling, virtual reality, and additive manufacturing in recent years. Unfortunately, it is known to be computationally expensive, especially if there are many parameters and data samples. To address this challenge, we propose to introduce the inexactness into descent methods, by iteratively solving a forward simulation step and a parameter update step in an inexact manner. The development of such inexact descent methods is centered at two questions: 1) how accurate/inaccurate can the two steps be; and 2) what is the optimal way to implement an inexact descent method. The answers to these questions are in our convergence analysis, which proves the existence of relative error thresholds for the two inexact steps to ensure the convergence. This means we can simply solve each step by a fixed number of iterations, if the iterative solver is at least linearly convergent. While the use of the inexact idea speeds up many descent methods, we specifically favor a GPU-based one powered by state-of-the-art simulation techniques. Based on this method, we study a variety of implementation issues, including backtracking line search, initialization, regularization, and multiple data samples. We demonstrate the use of our inexact method in elasticity measurement and design applications. Our experiment shows the method is fast, reliable, memory-efficient, GPU-friendly, flexible with different elastic models, scalable to a large parameter space, and parallelizable for multiple data samples.
Huamin Wang
Chief Scientist
My research interests include physics-based simulation and modeling, generative AI, numerical analysis and nonlinear optimization.